(5) Bayes’ theorem

Introduction

통계학에서 많이 응용되는 베이즈 이론에 대해 배워보고, 베이즈 이론의 한계와 머신러닝의 장점을 알아보자.

Pre-question

• 베이즈 정리란 무엇이고, 어떻게 쓰일 수 있을까?
• 베이즈 정리의 장단점은?

베이즈 정리

조건부확률의 정의에 따라 교집합을 다음과 나타낼 수 있다.

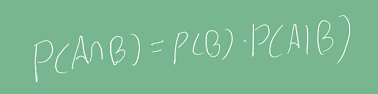
베이즈 정리는 수식적으로 **조건부확률을 이용해, A라는 새로운 정보가 주어질 때 P(B)로 부터 P(B

A)를 개산하는 방법을 알려준다.**

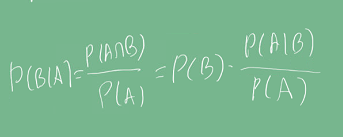
의미적으로는 사전확률을 통해 사후 확률을 계산할 때 쓰인다.

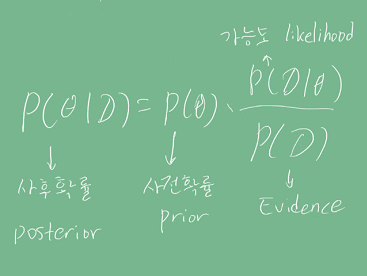
• D : 새로 관찰한 데이터
• θ: 우리가 모델링하는 이벤트 또는 계산하고 싶은 모델의 모수
• 사후확률 : 데이터가 주어진 상황 (관찰을 한 경우) 측정을 할 확률
• 사전확률 : 모델링 하기 이전에 이미 주어진 확률, 데이터를 분석하기 전에 가정한 확률
• 가능도 : 현재 주어진 파라미터(가정)에서 관찰된 확률을 계산하는 것.
• Evidence : 데이터 자체의 분포

예시를 들어보자. 코로나 바이러스 발병률이 10%고, 실제로 걸렸을 때 검진될 확률이 99%, 오검진 확률이 1%라고 할 경우,
P(θ) : 가정된 발병률 (hypothesis) = 10%
P(D|θ) : 실제로 걸렸을 때 검진 확률 = 99%
P(D|┑θ) : 실제로 걸리지 않았을 때 오검진 확률 = 1% *1종 오류라고 한다.

사후확률을 계산하기 위해 evidence를 먼저 계산해보자.

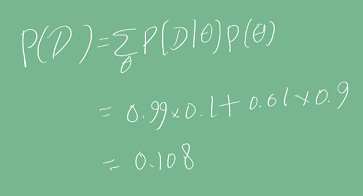
이 계산 결과를 이용해, 사후확률(검진 결과가 양성일 때, 실제 양성일 확률)을 계산해보자.

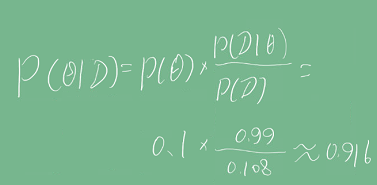
만약 1종 오류인 P(D|┑θ)이 10%로 오를 경우, P(D) = 0.189, P(θ|D) = 0.524로 상당히 올라가며, 테스트의 정밀도가 떨어지게 된다.

아래 혼동행렬을 참고하자.

여기서 False / True는 가정이 틀리고, 맞는지를 나타낸다.

중요한 것은, 베이즈 정리로 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전 확률로 사용해 갱신된 사후 확률을 계산할 수 있다는 것이다.

정밀도와 민감도

• Precision = TP / (TP + FP)로 계산된다. 예를 들면 날씨가 맑다고 예측한 결과 중 실제로 맑은 날의 비율이다.
• Recall : TP / (TP + TN)로 계산된다. 예를 들면 실제로 맑은 날 중, 모델이 맑다고 예측한 날의 비율이다.

이와 관련되어 아래 포스팅에 잘 정리되어있어 참고해도 좋을 것 같다. 링크

베이즈 추론

내용이 꽤 길어 정리할 시간이 없어(…) 링크 내용을 참고하면 좋을 것 같다. 베이즈 추론 링크

인과관계

인과관계는 데이터 분포의 변화에 강건한 예측 모형을 만들 때 필요하다. 인과관계를 추론할 때 베이즈 이론을 함부로 사용해서는 안된다.
예를 들어보자. 요소 T, Z, R이 있고 이 요소들은 특정 요소에 영향을 미칠 수 있다. R은 지능지수, T는 키라고 하자. 통계적으로 T인 키가 클 경우, 지능지수 R이 높게 나온다고 한다. 이 경우, R은 T에 정비례 관계가 있다고 말할 수는 있다.
그러나, 키가 직접적으로 지능 지수를 높게 하는 원인이라고 할 수 있을까? 실제로는 그렇지 않은데, 바로 중첩효과 때문이다.

• 충첩효과(confounding factor) : 현상에서 가정한 독립변수(T)와 종속변수(R)에 모두 영향을 미치는 변수가 존재할 때 이를 중첩효과라고 한다.

예시로 설명하자면 Z, 나이라는 요소가 T, R에 모두 영향을 미치기 때문에 T->R의 인과관계가 있다고 오인한 것이다.

R을 지능지수,T가 키라고 하면, 중첩요인인 Z의 효과를 제거하지 않으면 가짜 연관성이 나온다. 연령이라는 중첩효과를 제거하지 않았기 때문이다.

따라서 인과관계를 알기 위해서는 이런 중첩효과를 모두 제거해야 한다. 그렇기 때문에 사실 인과관계를 알아내기가 쉽지 않다.

중첩효과로 인한 문제를 다음 예시에서 좀 더 확인할 수 있다.

• 신장결석에 걸린 사람을 치료할 수 있는 치료법이 a, b 두 개가 있다고 하자. T는 치료법[a,b]이고 R은 완치율이다. 그리고 신장 결석 크기를 Z라고 하자.

치료법	전체 완치율	small stones에 대한 완치율	large stones에 대한 완치율
a	78% (273/350)	93% (81/87)	73% (192/263)
b	83% (289/350)	87% (234/270)	69% (55/80)

치료법 a,b에서 전체 완치율만 놓고 보면 b가 좋아보인다.
그러나, 신장결석 크기에 따른 조건부 확률로 계산해 보면 a가 더 좋고, 실제로 a가 더 좋은 치료법이다.
조건부 확률로 계산한 치료효과가 do(T=a)라는 조정(intervention) 효과를 통해 Z의 개입을 제거하기 때문이다.

Discussion

• 베이즈 정리는 기계공학에서 물체의 위치/방향을 추정하기 위한 칼만필터에서도 쓰인다. 링크
• 베이즈 정리로 스팸 메일을 분류하는 데 쓰일 수 있다. 그러나 딥러닝을 사용한 방법이 더 좋은 결과를 내는 데, 왜 그런지 베이즈 정리의 한계로 설명할 수 있으면 좋을 것 같다.

Reference

• 네이버 AI 부트캠프 (* 강의 자료 바탕으로 재구성)
• 중첩효과